Nombres complexes
Les nombres complexes reposent sur la définition de la quantité
.
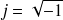Un nombre complexe est défini par
,
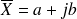et
ét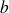ant des réels. On indique qu'un nombre est à priori complexe en le surlignant.
a est appelé partie réelle de
,
b est appelé partie imaginaire de
.
On désigne par module de
la quantité
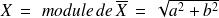
et par argument de
, l'angle
tel que
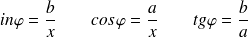
Les opérations sur les nombres complexes s'apparentent aux opérations sur les vecteurs.
Au nombre complexe
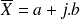on peut associer le vecteur
dans un plan muni d'un repère orthonormé
.
Par ailleurs, on sait que
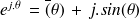
Donc, notre nombre complexe
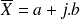peut aussi s'écrire
.
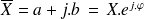
Nous avons donc le choix entre deux expressions : l'une mettant en évidence les parties réelles et imaginaires et l'autre mettant en évidence le module et l'argument.
