Conception de formes de relecture dans les chaînes éditoriales numériques

Le plus long chemin d'un graphe peut être calculé à l'aide de l'algorithme de Bellman. Pour aborder ce problème, nous nous appuierons sur un exemple d'utilisation de la méthode potentiel-tâche utilisée en gestion de projet industriel. Cet exemple, bien que n'ayant rien à voir avec notre cadre documentaire, nous permettra d'illustrer plus facilement la notion de plus long chemin à l'aide d'un cas d'application assez classique.

La méthode potentiel-tâche permet notamment de déterminer la durée théorique d'un projet à partir des durées de réalisation des tâches de ce projet ainsi que des contraintes de succession entre ces tâches. Soit l'exemple suivant, à partir duquel nous allons appliquer cette méthode :

Le graphe ci-dessous est construit à partir des données du tableau des tâches. Les nœuds du graphe représentent les tâches, tandis que les liens indiquent les contraintes de succession entre tâches. Chaque lien est valué par la durée de la tâche de son nœud d'origine. Enfin, deux tâches fictives représentant respectivement le début (α) et la fin (ω) du projet sont ajoutées au graphe (les liens partant du nœud α sont valués à 0).

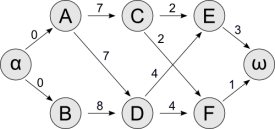
Pour chaque tâche, on cherche à connaître ses dates de réalisation au plus tôt et au plus tard, afin de savoir si un retard sur cette tâche est critique par rapport au projet global. Ces dates sont exprimées relativement à la date de début du projet, fixée à 0. Par exemple, si une tâche a pour date au plus tôt 8 et pour date au plus tard 10, elle a une marge de deux semaines en cas de retard de réalisation. En revanche, si les dates au plus tôt et au plus tard sont égales, cette tâche est critique car tout retard aura un impact sur la durée globale du projet. Pour déterminer la date au plus tôt d'une tâche, on procède par comparaison de la somme des durées sur chaque chemin permettant d'accéder à cette tâche depuis la tâche α. En effet, parmi les différents chemins possibles entre deux mêmes tâches, c'est celui correspondant à la durée maximale qui doit l'emporter. Par exemple :

• la date au plus tôt de A est 0 car il n'y a qu'un seul chemin pour l'atteindre depuis α, valant 0 (idem pour B) ;

• la date au plus tôt de C est 7 car il n'y a également qu'un seul chemin pour l'atteindre, valant 7 (0 + 7) ;

• la date au plus tôt de D est 8, en suivant le chemin α-B-D (0 + 8 = 8) plutôt que α-A-D (0 + 7 = 7) ;

• la date au plus tôt de F est 12, en suivant le chemin α-B-D-F (0 + 8 + 4 = 12) plutôt que α-A-D-F (0 + 7 + 4 = 11) ou encore α-A-C-F (0 + 7 + 2 = 9) ;

• ... et ainsi de suite en parcourant tous les nœuds : E et finalement ω ont pour date au plus tôt 12 et 15 ;

• ainsi, le projet global aura une durée de 15 semaines (s'il n'y a pas de retard).

Notons que la date au plus tôt d'une tâche i, notée ti, est définie formellement comme suit : ti = Max(tj + dj), avec :

• j appartenant à l'ensemble des nœuds précédant i ;

• dj étant la durée de j ;

• la tâche initiale t0 ayant pour date au plus tôt 0.

Le problème illustré par cet exemple correspond en fait à la recherche d'un chemin le plus long (par somme des valeurs des liens) entre deux nœuds d'un graphe. En effet, les dates au plus tôt de chaque tâche correspondent à la longueur du chemin le plus long entre α et le nœud représentant cette tâche. Si l'on parcourt le graphe à l'envers (de ω à α) en choisissant à chaque fois la nœud précédant de sorte que la somme de sa date au plus tôt et de sa durée soit égale à la date au plus tôt du nœud courant, on obtient le chemin le plus long dans le graphe : de ω, on va en E (12 + 3 = 15) ; de E, on va en D (8 + 4 = 12)... jusqu'à obtenir α-B-D-E-ω comme plus long chemin. Notons, sans nous attarder sur ce point, que les dates au plus tard de chaque tâche peuvent également être déterminées par un parcours inverse du graphe.

L'algorithme de Bellman permet de rechercher les plus courts chemins entre deux nœuds d'un graphe orienté sans circuit (GOSC) et dont les arcs sont pondérés. Il est classiquement appliqué pour des problèmes d'optimisation : par exemple, on cherche à minimiser le coût du trajet entre deux villes entre lesquelles plusieurs itinéraires sont possibles (les arcs du réseau routier sont par exemple pondérés en fonction du nombre de kilomètres, du prix des péages, etc.). C'est l'adaptation de cet algorithme à la recherche des plus longs chemins qui nous intéresse ici.

Cet algorithme repose sur le principe de relaxation, que l'on peut expliquer comme suit. Soient :

• p[] le tableau des poids de chaque arc ;

• d[] le tableau de distance de chaque sommet à S0, initialisé avec d[S0] = 0 et d[Si] = -∞ pour tout i différent de 0 ;

• pred[] le tableau des prédécesseurs de chaque sommet sur le plus long chemin, initialisé à null pour tous les sommets.

relaxation(u, v) {

	si d[u] + p[u,v] > d[v] alors d[v] = d[u] + p[u,v]

	pred[v] = u

}

relaxation(u, v) {
	si d[u] + p[u,v] > d[v] alors d[v] = d[u] + p[u,v]
	pred[v] = u
}

L'idée de l'algorithme est la suivante :

• étant donné un sommet u, la procédure relaxation(u, v) est appelée pour tous les sommets v adjacents à u ;

• le traitement précédent est répété sur chaque sommet ordonné suivant un tri topologique (c'est-à-dire qu'un sommet sera toujours traité avant ses successeurs) ;

• une fois tous les nœuds traités, on peut reconstruire le(s) plus long(s) chemin(s) en suivant les prédécesseurs depuis le sommet final dans le tableau pred[].

Notons que si les sommets ne sont pas ordonnés selon un tri topologique, le traitement devra être répété jusqu'à ce que la relaxation ne fasse plus effet.

Nous illustrons le déroulement de cet algorithme à l'aide du graphe et du tableau ci-dessous. Dans le tableau, les valeurs successives sont séparées par des slashs. On remarque que la distance du sommet A au sommet E a été relaxée deux fois. Le chemin le plus long de ce graphe est donc A-B-D-E.

Le tableau ci-dessous donne le résultat de l'exécution de l'algorithme sur ce graphe. Les valeurs successives des distances et des prédécesseurs sont séparées par des slashs. On remarque que la distance du sommet A au sommet E a été relaxée deux fois. Le chemin le plus long de ce graphe est donc A-B-D-E.

Pour appliquer l'algorithme de Bellman dans notre contexte, il est nécessaire de valuer les liens entre les nœuds du graphe : une méthode triviale consiste à attribuer la valeur 1 à tous les liens. Il convient également d'ajouter une étape fictive ω liée par toutes les étapes finales (20 et 21 dans le graphe d'Un conte à votre façon), ainsi que de supprimer les liens provoquant des circuits (le lien allant de 8 à 7 dans notre exemple). De cette façon, nous pouvons calculer les distances maximales de l'étape 1 à toutes les autres étapes puis en déduire un ou plusieurs plus longs chemins de 1 à ω, en nous basant sur la même démarche que celle de l'exemple de la méthode potentiel-tâche.