Fonctions localement intégrables
On considère un intervalle
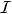 de
de
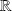 qui n'est ni vide, ni réduit à un point et qui n'est pas un intervalle fermé borné. Il est donc d'un des types énumérés plus haut. On considère une fonction
qui n'est ni vide, ni réduit à un point et qui n'est pas un intervalle fermé borné. Il est donc d'un des types énumérés plus haut. On considère une fonction
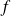 réelle définie sur
réelle définie sur
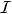 . On supposera
. On supposera
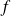 localement intégrable sur
localement intégrable sur
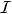 .
.
Définition : Définition
Une fonction
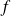 localement intégrable sur
localement intégrable sur
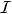 est une fonction intégrable sur tout intervalle fermé borné contenu dans
est une fonction intégrable sur tout intervalle fermé borné contenu dans
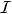 .
.
Par exemple si
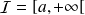 cela signifie que, pour tout
cela signifie que, pour tout
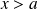 , l'intégrale existe
, l'intégrale existe
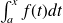 , ou encore que la fonction
, ou encore que la fonction
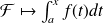 est définie sur l'intervalle
est définie sur l'intervalle
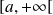 .
.
Exemple :
la fonction
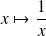 est localement intégrable sur les intervalles
est localement intégrable sur les intervalles
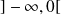 et
et
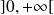 ;
;la fonction logarithme est localement intégrable sur l'intervalle
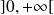 ;
;la fonction
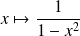 est localement intégrable sur les intervalles
est localement intégrable sur les intervalles
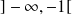 ,
,
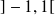 et
et
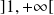 .
.





