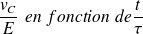Mise sous tension

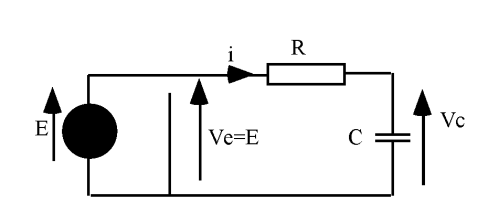
Nous allons maintenant étudier un circuit constitué d'un condensateur 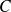en série avec une résistance 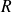, le tout étant alimenté par un échelon de tension 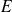appliqué à .

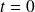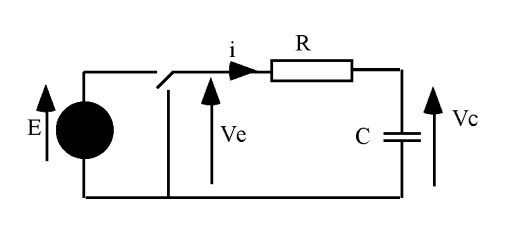
Le condensateur donne entre la tension 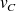à ses bornes et le courant 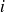qui le traverse la relation

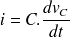
De ce fait, pour arriver à une équation différentielle et non pas intégrale, nous allons choisir comme variable la tension 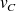aux bornes du condensateur et remplacer partout 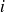par .

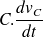La mise en équation donne :

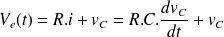
Jusqu'à 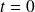, 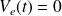et à partir de ,

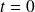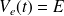
Il faut donc résoudre l'équation différentielle :

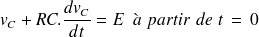
C'est encore une équation différentielle linéaire du 1er ordre à coefficients constants, avec second membre.

• La solution générale de l'équation sans second membre

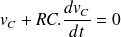
est

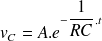
• Une solution particulière évidente de l'équation avec second membre est celle qui correspond à 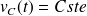, donc :

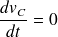Donc, la solution générale complète de notre équation différentielle est :

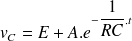
La grandeur 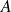est trouvée en tenant compte des conditions initiales. Aux bornes du condensateur 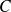, la tension 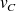ne peut pas être discontinue. Donc, si le circuit est parti d'un état de repos, jusqu'à 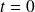, 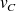était égal à 0. Juste après l'instant 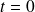, 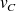doit toujours être égal à 0.

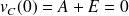
Donc

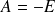
et

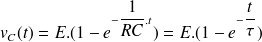
avec

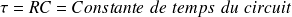
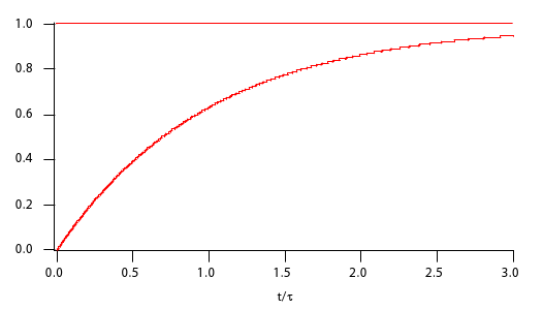
La tension s'établit donc exponentiellement, avec la constante de temps 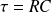. On appelle cela la charge du condensateur. C'est le résultat fondamental à retenir.