Gradient

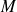Soit dans une région de l'espace une grandeur scalaire définie en tout point (par exemple la température en tout point d'une pièce). Dans un repère orthonormé, le point 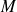a pour coordonnées 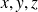et est une fonction de ces trois coordonnées : 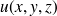. Si la fonction 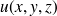est continuement dérivable, on appelle gradient de la grandeur vectorielle

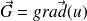
définie par ses composantes :

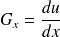
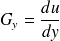
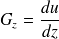
On a ainsi introduit un vecteur défini en tout point, c'est à dire un champ de vecteur .
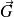