Circulation du gradient

Pour un déplacement élémentaire 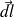, on appelle circulation du vecteur 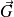le produit scalaire .

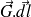Si le déplacement élémentaire 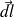a pour coordonnées 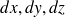, ce produit scalaire vaut

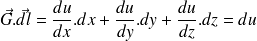
Les deux relations

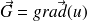
et

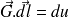
sont donc équivalentes.On dit que le champ 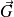dérive de la fonction .

Le champ se dirige dans le sens des croissants.

On peut dire que le vecteur 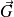indique la direction et l'importance de la croissance de . (Exemple : un gradient de température)

NB1 : Si dans un volume donné 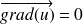, c'est que la quantité est uniforme.

NB2 : Le gradient n'est défini que si la fonction 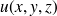est dérivable.