Il faut distinguer différents cas, selon la position relative du point et de la sphère.
Sphère vue d'un point intérieur
1) Si le point M est à l'intérieur de la sphère, la surface interne de celle-ci occupe tout l'horizon. Donc
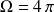 .
.
Sphère vue d'un point de sa surface
2) Si le point
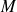 est juste sur la surface de la sphère, elle lui cache exactement la moitié de l'horizon. Donc
est juste sur la surface de la sphère, elle lui cache exactement la moitié de l'horizon. Donc
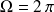 .
.
Sphère vue d'un point extérieur
3) Si le point
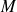 est à l'extérieur de la sphère
est à l'extérieur de la sphère
On peut écrire
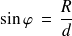
donc
On peut alors utiliser la relation démontrée précédemment:
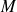 est à l'extérieur de la sphère
est à l'extérieur de la sphère
Application : Calculer l'angle solide sous lequel on voit le soleil et la lune depuis la terre.
Le soleil vu de la terre :
Distance terre - soleil : (centre à centre)
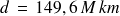 minimum (152,1 M km maximum)
minimum (152,1 M km maximum)
Rayon du soleil : 696000 km
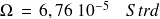
La lune vue de la terre :
Distance terre - lune : (centre à centre)
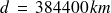
Rayon de la lune : 1738 km
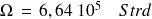
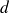 de son centre ?
de son centre ?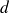 de son centre ?
de son centre ?