Exemple avec Loi de Moore
Illustrons cela par un exemple
Gordon Moore, cofondateur de la Société Intel, annonça en 1965 que le nombre de transistor par circuit de même surface allait doubler tous les 18 mois ce qui conduirait à une augmentation exponentielle de ce nombre de transistor en fonction du temps. Affirmation très optimiste, mais observons l'évolution réelle de ce nombre de transistors par circuit au fil des années[1].
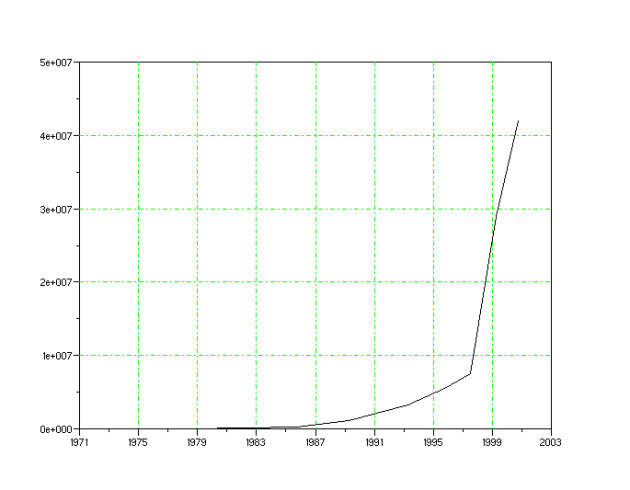
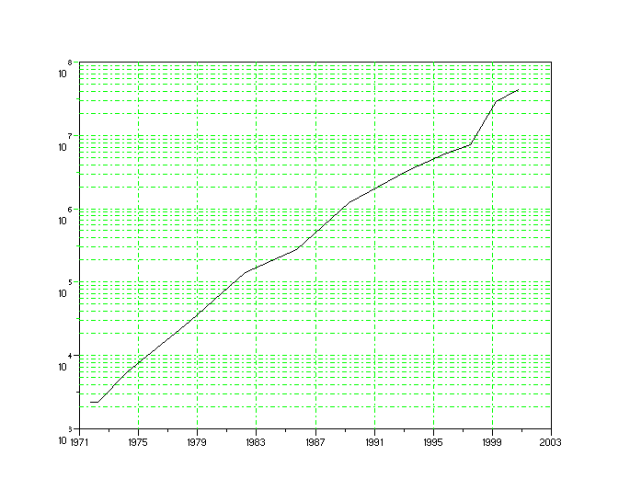
Ce tracé[1] est inutilisable car toutes les valeurs de 1971 à 1985 sont trop faibles pour apparaître clairement, mais si l'on modifie l'axe du nombre de transistor en le remplaçant par son logarithme[2], nous observons les valeurs de toutes les années et la pseudo-linéarité du graphique nous permet de confirmer l'évolution exponentielle du nombre de transistors disponibles sur une même surface de circuit.
Selon les lois mathématiques utilisées pour représenter les données, il est donc possible de réaliser des changements d'axe ou de variables afin d'obtenir une représentation graphique linéaire de ces données. L'avantage est qu'il devient alors facile de déterminer graphiquement la pente et l'ordonnée à l'origine de la droite ainsi obtenue. Ces deux valeurs donnent ensuite accès aux paramètres de la loi mathématique représentative des données.
Dans ce qui suit, quelques lois mathématiques couramment utilisées en chimie et en physique, sont présentées.