Utilisation de graphiques à échelle(s) logarithmique(s)
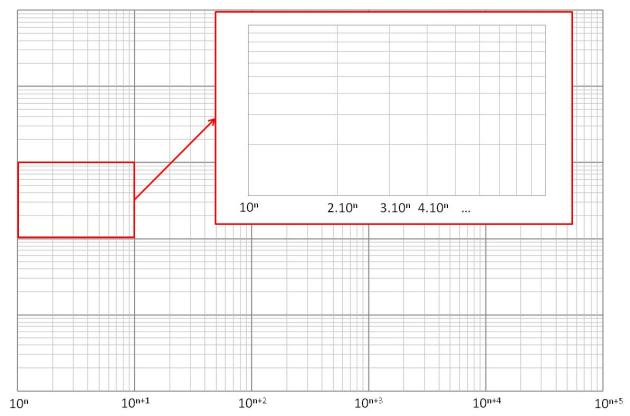
La figure suivante représente une grille dont les graduations suivent une progression logarithmique aussi bien horizontalement que verticalement grille (log/log). Les graduations principales représentent des décades, ce qui signifie que d'une graduation principale à la suivante, la valeur correspondant à ces graduations est multipliée par 10. En d'autres termes, les graduations principales correspondent à des puissances de 10, la valeur de la puissance augmentant de 1 à chaque décade. Ceci est illustré sur la figure, au niveau de l'axe des abscisses, en prenant comme première valeur 10n.
On peut en outre noter que la valeur de n peut être positive et négative, et que son choix dépend des plages de valeur que l'utilisateur a besoin de faire figurer sur le graphique. D'autre part, dans le cas d'une grille log/log (comme ici), l'axe horizontal et l'axe vertical n'auront pas nécessairement la même puissance de 10 pour leur première valeur.
A l'intérieur de chaque décade, il apparaît des subdivisions. Chaque subdivision est un multiple de la puissance de 10 à laquelle la décade se réfère : si la décade débute avec une valeur 10n, la première subdivision correspond à 2.10n, la deuxième à 3.10n, ... jusqu'à la neuvième subdivision qui correspond à 9.10n.
Une fois les graduations clairement identifiées, on place les points sur le graphe en utilisant directement les valeurs x et y, la progression logarithmique des valeurs étant prise en compte par la graduation elle-même. Lorsque les valeurs à placer correspondent à une des graduations, il n'y a aucune difficulté pour placer les points. En revanche, lorsque les valeurs se situent entre deux graduations, il est difficile de placer le point avec exactitude puisque il faut considérer une progression logarithmique des valeurs entre des graduations consécutives. Il en résulte une certaine approximation dans le positionnement des points sur le graphe.
Lorsque l'on utilise des échelles logarithmiques afin de mettre en évidence une corrélation linéaire apparente au niveau du graphe, il est souvent intéressant de déterminer la pente et l'ordonnée à l'origine de cette relation linéaire. Pour obtenir graphiquement ces deux valeurs, il ne faut pas oublier que la linéarité tient compte de la progression logarithmique des valeurs. Par exemple, si les échelles des abscisses (x) et des ordonnées (y) sont toutes les deux logarithmiques, et qu'il apparaît que les points du graphe s'alignent sur une droite moyenne, la relation linéaire existe entre log(x) et log(y), et non pas entre x et y directement. Si on considère deux points A et B de la droite moyenne, de coordonnées respectives (xA ;yA) et (xB ;yB), la pente P de cette droite sera obtenue par l'équation suivante :
\(P=\frac{\log {{y}_{B}}-\log {{y}_{A}}}{\log {{x}_{B}}-\log {{x}_{A}}}\)
NB : cette relation n'est valable que si les deux échelles en x et y suivent une progression logarithmique
Ce calcul de pente peut donc se faire en relevant les coordonnées de A et B sur le graphe, puis en calculant les logarithmes décimaux de ces valeurs.
L'autre possibilité consiste à passer de l'échelle logarithmique à une échelle linéaire. Pour cela, on peut tout simplement utiliser une règle graduée. On commence par mesurer la longueur d'une décade ; cette longueur est proportionnelle à \((\log {{10}^{n+1}}-\log {{10}^{n}})\) donc à 1. Ensuite, on mesure la distance entre le point d'origine de la décade et la coordonnée x (resp. y) sur l'axe des abscisses (resp. des ordonnées) ; cette nouvelle mesure est proportionnelle à \((\log x-\log {{10}^{n}})\), soit \((\log x-n)\). Il suffit ensuite de réaliser un produit en croix pour retrouver la valeur de \((\log x-n)\), ce qui permet de déduire la valeur de log(x).
Pour la détermination de l'ordonnée à l'origine b, une fois la pente P obtenue, il suffit de considérer un point de la droite, puis d'utiliser l'équation de la droite. Par exemple, on prend le point A et on a :
\(\log {{y}_{A}}=P\log {{x}_{A}}+b\)
D'où :
\(b=\log {{y}_{A}}-P\log {{x}_{A}}\)