Chapitre 3 : Exploitation graphique de résultats

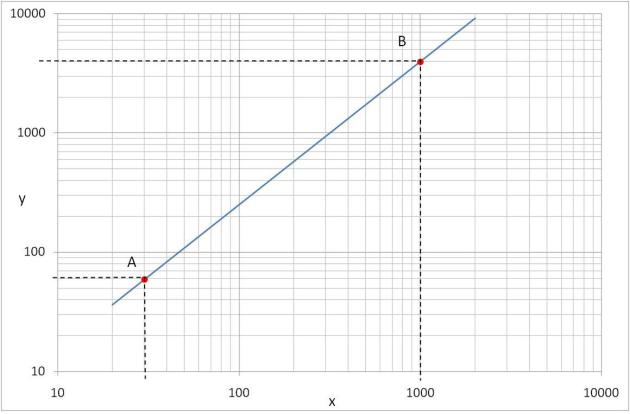
Référez vous à la représentation x-y sur graphique log-log^[1]. Sur cette représentation, il apparaît une droite dont on doit déterminer la pente. Deux points A et B de la droite ont été choisis. On peut lire leurs coordonnées directement sur le graphique : A (30 ; 60) et B (1000 ; 4000).

On calcule alors la pente P de la droite : \(P=\frac{\log 4000-\log 60}{\log 1000-\log 30}=1,2\)

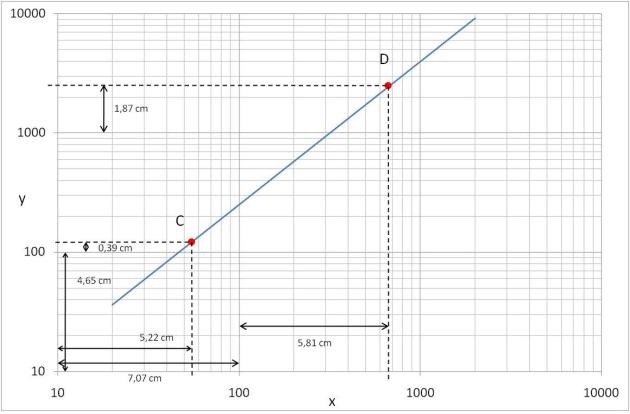
On reprend le même exemple mais en considérant deux points C et D distincts de A et B (figure suivante^[2]) ; cette fois, on va utiliser des mesures via une échelle linéaire (les distances mesurées sont indiquées). Sur l'axe des abscisses, une décade mesure 7,07 cm ce qui est proportionnel à \((\log {{10}^{n+1}}-\log {{10}^{n}})\).

Pour le point C, la distance entre le début de la décade (10) et x_C est égal à 5,22 cm, ce qui est proportionnel à\( (\log {{x}_{c}}-\log 10)\) .

Finalement, on peut écrire : \((\log {{10}^{n+1}}-\log {{10}^{n}})\times 5,22=(\log {{x}_{c}}-\log 10)\times 7,07\)

\((n+1-n)\times 5,22=(\log {{x}_{c}}-1)\times 7,07\)

\(\log {{x}_{c}}=\frac{5,22}{7,07}+1\)

Si on fait les mêmes calculs pour le point D, on obtient :

\(\log \ {{x}_{D}}=\frac{5,81}{7,07}+2\)

Pour l'axe des ordonnées, on reprend la même méthodologie et on obtient :

\(\log \ {{y}_{C}}=\frac{0,39}{4,65}+2\)

\(\log \ {{y}_{D}}=\frac{1,87}{4,65}+3\)

Ensuite, on calcule la pente :

\(P=\frac{\log {{y}_{{}}}-\log {{y}_{C}}}{\log {{x}_{D}}-\log {{x}_{C}}}=1,22\)

Avec les deux méthodes, les résultats sur la pente sont bien du même ordre de grandeur.

Autre exemple (à traiter par vous-même) :

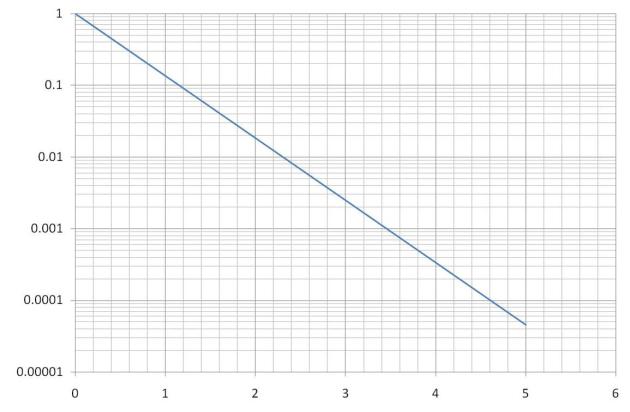
La figure 21 représente le tracé d'une fonction du type \(y={{e}^{kx}}\). Ce tracé a été effectué sur une représentation semi-logarithmique (échelle linéaire pour les abscisses et logarithmiques pour les ordonnées). En effet, pour linéariser la fonction ci-dessus, on trace log(y) en fonction de x, soit :*

\(y=k(\log e)\times x\)

L'objectif est de trouver la valeur de k (réponse : k = -2)