Régime propre
Lorsque le circuit
est court-circuité sur lui même,
.
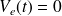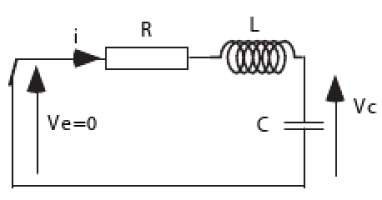
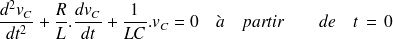
Posons
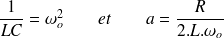
L'équation devient :
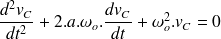
La solution de cette équation différentielle (voir cours de mathématiques) dépend du déterminant de l'équation caractéristique associée.
-
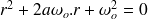
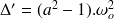
1er cas : Si
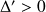, les racines sont :
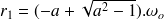
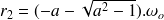
Dans ce cas, la solution générale de l'équation différentielle est
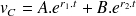
Cela suppose donc que
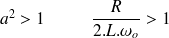
donc
Puisque la tension
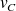vaut
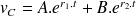
le courant
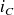s'écrit
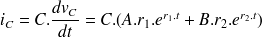
Les quantités A et B dépendent des conditions initiales :
Ainsi, si on part d'un courant nul et d'une tension
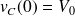, c'est-à-dire si on ferme sur lui-même un circuit
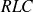dont le condensateur possédait une charge initiale
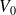et qui était au départ en circuit ouvert, nous aurons :
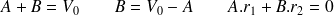
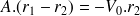
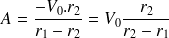
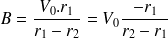
D'où
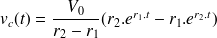
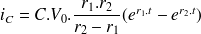
Ce type de fonctionnement est dit apériodique.
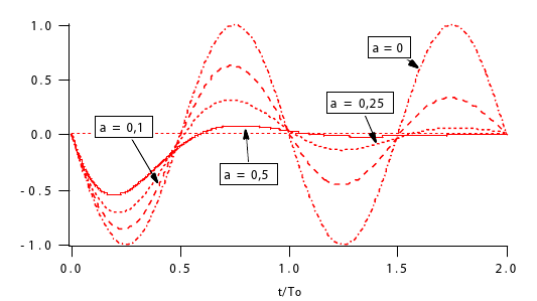
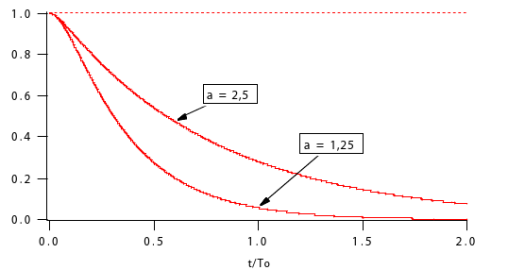
Les formes d'onde sont les suivantes :
Les premières courbes montrent l'évolution de la tension relative
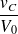en fonction du temps relatif
.
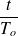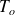étant la période propre du circuit =
.
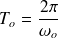Elle a été tracée pour deux valeurs de a.
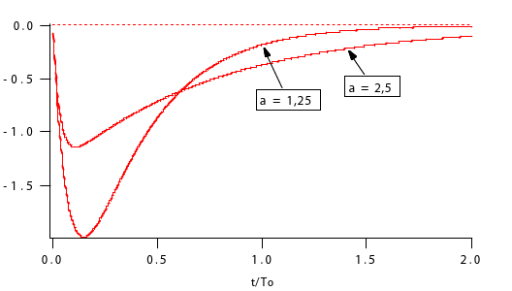
Les courbes suivantes montrent l'évolution du courant relatif
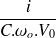en fonction du temps relatif
.
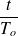Elle a été tracée pour les deux mêmes valeurs de a que précédemment.
-
2ème cas : Si
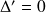, c'est-à-dire si
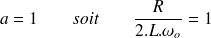
donc
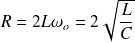
alors, l'équation associée présente une racine double :
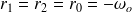
et la solution de l'équation différentielle est
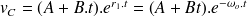
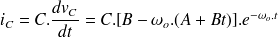
Avec les mêmes conditions que précédemment, on obtient :
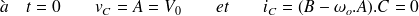
donc
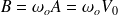
d'où
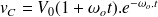
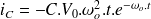
Ce cas particulier est dit régime critique.
Les formes d'onde sont assez semblables à celles du régime précédent.
La première courbe montre l'évolution de la tension relative
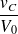en fonction du temps relatif
.
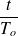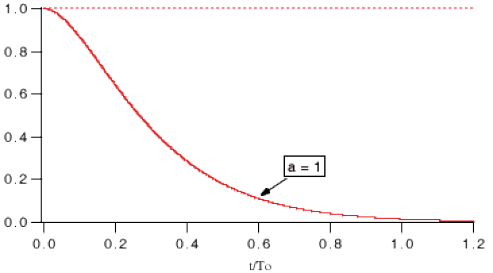
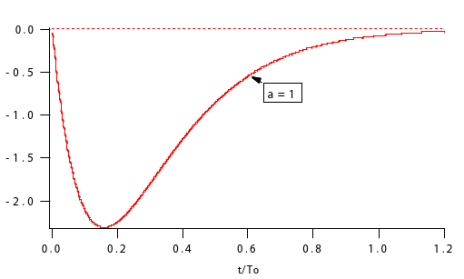
La courbe suivante montre l'évolution du courant relatif
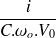en fonction du temps relatif
.
-
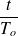3ème cas : Si
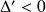, c'est-à-dire si
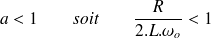
donc
dans ce cas, la solution de l'équation différentielle est donnée par :
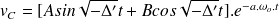
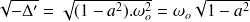
Désignons par
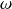cette quantité.
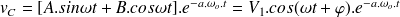
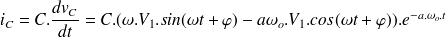
ou
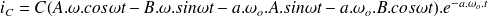
Ainsi, si à
,
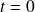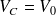et
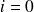, on obtient :
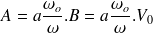
L'expression du courant est donc:
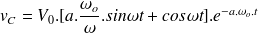
L'expression du courant est :
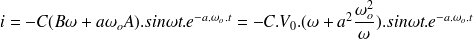
donc
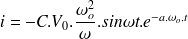
Le courant et la tension subissent donc des évolutions sinusoïdales avec amortissement exponentiel.
La pulsation de ces oscillations vaut
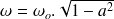
et l'amortissement exponentiel est en
.
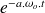Ce fonctionnement est dit régime sinusoïdal amorti.
Le circuit est dit oscillant.
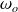est appelée pulsation de résonance ou pulsation propre du circuit oscillant.
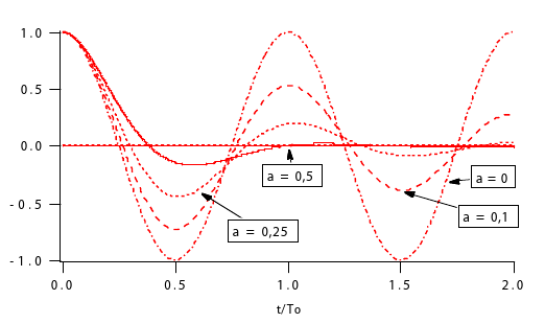
Les formes d'onde sont indiquées ci-après
La première courbe montre l'évolution de la tension relative
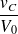en fonction du temps relatif
.
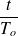La courbe suivante montre l'évolution du courant relatif
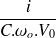en fonction du temps relatif
.
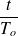