Champ créé sur l'axe d'une spire circulaire.
En un point M de l'axe,
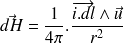
Le module
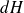de
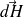vaut
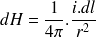
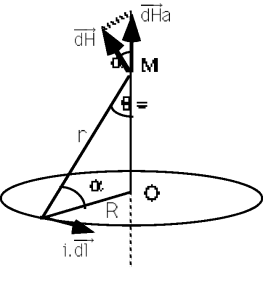
Calcul du champ sur l'axe d'une spire circulaire
Les
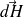créés par tous les
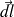qui constituent la spire ont une résultante qui est portée par l'axe.
Donc nous allons additionner les projections
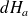de
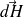sur cet axe.
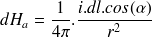
avec
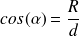
Donc,
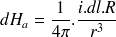
Par intégration, on obtient le champ résultant :
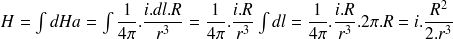
Si on est dans le vide ,
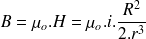
On peut exprimer ce résultat en fonction de l'angle
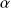
ou en fonction de
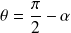
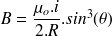
Au centre de la spire,
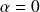donc
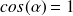et
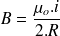
Le sens de
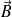peut être retrouvé aisément par le moyen mnémotechnique suivant : Si l'on imagine un tire bouchon tournant dans le sens du courant, il progresse dans le sens du champ magnétique.
