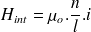Exemple n 2 : Champ créé par un solénoïde infiniment long

Prenons maintenant le cas d'un solénoïde infini constitué de spires jointives s'appuyant sur un cylindre de section quelconque.

Par raison de symétrie, 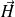en tout point est parallèle à la direction 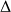du solénoïde. Les lignes de champ sont des droites parallèles à .

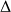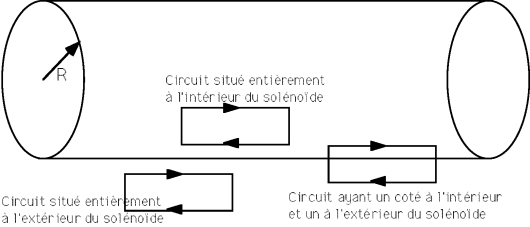
Si on applique le théorème d'Ampère à un parcours rectangulaire dont deux cotés de longueur 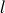sont parallèles à ,

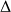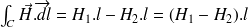
1 - Si ce parcours est entièrement intérieur au solénoïde, il n'encercle aucun courant. Donc

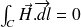
Cela prouve que

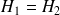
Donc le champ 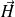est uniforme partout à l'intérieur du solénoïde.

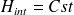
2 - Si ce parcours est entièrement extérieur au solénoïde, il n'encercle aucun courant. Donc

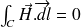
Cela prouve encore que

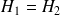
Donc le champ 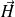est uniforme partout à l'extérieur du solénoïde. 

Or infiniment loin du solénoïde 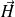est nul.

Donc, c'est que 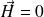partout à l'extérieur du solénoïde.

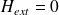
3 - Si ce parcours a un coté extérieur au solénoïde et l'autre intérieur, il encercle une quantité de courant proportionnelle à sa longueur 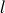: Si on désigne par le nombre de spires encerclées dans la longueur 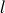et par 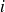le courant dans une spire, alors le courant encerclé par le parcours vaut 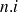. Donc

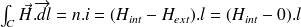
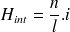
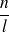est le nombre de spires par unité de longueur.

Dans le vide,