Chapitre 3 : Exploitation graphique de résultats

Soit la courbe représentée ici^[1]. Elle représente l'influence du pH sur un potentiel d'électrode.

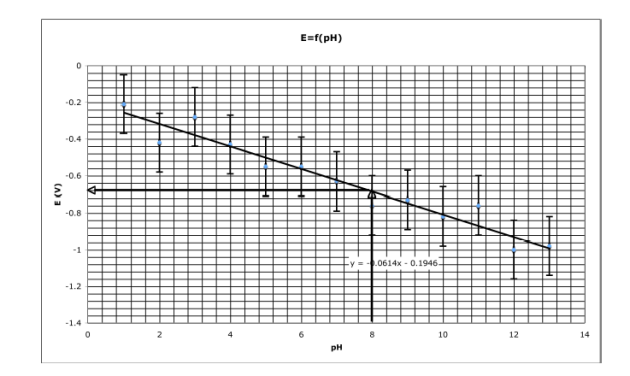
Supposons que l'on désire connaître le potentiel d'électrode et son incertitude correspondant à un pH de 8. En traçant la meilleure droite, qui doit impérativement passer par tous les carrés^[1] d'incertitude, on peut déterminer graphiquement que le potentiel d'électrode est égal à -0,68 V.

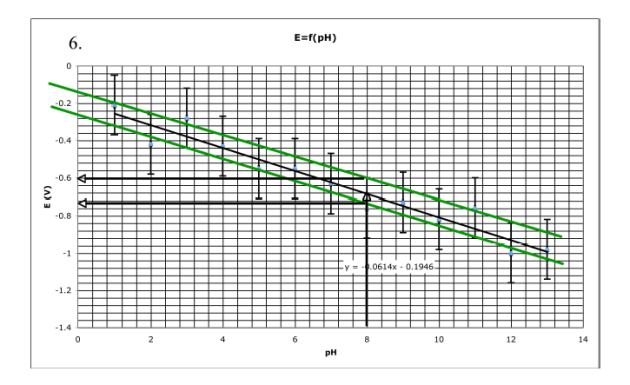
L'incertitude sur ce potentiel d'électrode est déterminée en traçant deux droites^[2] extrêmes dites "parallèles^[3]". La première est la droite la plus haute passant par tous les carrés d'incertitude, la deuxième est la plus basse passant par tous les carrés d'incertitude. Ces deux droites permettent de déterminer deux valeurs extrêmes de potentiels qui encadrent la valeur "moyenne". On peut lire graphiquement une valeur minimale d'environ -0,74 V et une valeur maximale d'environ -0,60 V. On peut remarquer que la valeur moyenne n'est pas exactement centrée par rapport à l'intervalle d'incertitude; mais elle est proche. Pour obtenir la valeur de l'incertitude, on calcule les différences entre la valeur moyenne et les valeurs extrêmes, et on retient la plus grande de ces deux différences (en valeur absolue). Dans ce cas, on peut supposer que le potentiel d'électrode est égal à -0,68 ± 0,08 V. Si la valeur moyenne est très décentrée, le calcul d'incertitude ne peut être systématique et est rendu compliqué. Cette situation n'est pas traitée dans ce document car peu rencontrée en TP.