Circuits électriques linéaires complexes en courant continu
Etudions d'abord le cas où le circuit ne comporte que des sources de tension et des résistances et pas de sources de courant.
Un réseau contient
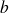branches et
noeuds ;
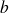est forcément
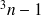. L'application de la loi de Kirchhoff aux noeuds donne n équations de noeuds qui ne sont pas indépendantes : Elle donne
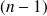équations indépendantes.
Ainsi, à partir des
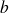courants de branches et de ces
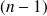relations, il reste
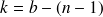inconnues. Pour trouver ces inconnues, on doit chercher
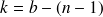mailles indépendantes auxquelles on applique la loi de Kirchhoff aux mailles.
Exemple : Le pont de Wheatstone
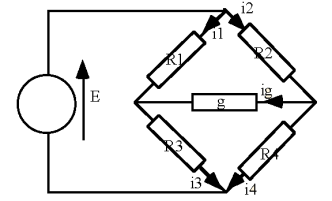
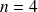noeuds
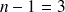équations de noeuds.
6 branches
3 courants indépendants : par ex :
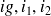
Les équations de noeud sont utilisées au fur et à mesure de la définition des courants pour introduire le moins possible d'inconnues. Chaque maille indépendante nous donne une équation où interviennent les courants indépendants
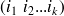et les fem rencontrées dans la maille, du genre
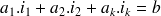
où les
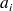sont homogènes à des résistances (en
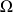) et
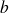homogène à une fem (en v). L'ensemble des
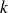équations indépendantes constitue donc un système matriciel. La résolution d'un tel système a été vue en cours de mathématiques. Elle nous donne la valeur de tous les courants.
Voyons maintenant le cas où l'une des branches du circuit contient une source de courant. Dans ce cas, la valeur du courant dans cette branche est connue et nous avons une inconnue de moins. Mais par ailleurs, la source de courant n'impose pas la tension à ses bornes. Nous avons donc également une équation de moins. Le système reste donc cohérent. A chaque extrémité de la source de courant,
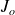intervient dans la définition d'un des courants du réseau. Ainsi, dans l'écriture de la loi de Kirchhoff sur les mailles indépendantes, nous verrons apparaître des équations du genre :
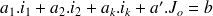
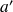étant, comme les
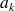, homogène à une résistance. Le système complet des équations devient alors du type :
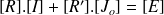
Dans le cas le plus général d'un réseau linéaire en courant continu, on peut avoir plusieurs sources de courant en plus des sources de tension et des résistances et on aboutit à la formulation générale suivante.
