Conception de formes de relecture dans les chaînes éditoriales numériques

Les algorithmes de diff ont pour fondement théorique le problème de la distance d'édition (edit distance en anglais). Il s'agit de mesurer la similarité entre deux chaînes de caractères C1 et C2, ou encore entre deux arbres A1 et A2, en cherchant un ensemble minimum d'opérations (edit script) permettant de transformer S1 en S2, respectivement A1 en A2.

L'algorithme de Levenshtein (1966^[1]) recherche la distance de deux chaînes C1 et C2 en évaluant le coût minimal d'édition en termes d'ajout, de suppression et de substitution de caractères. Par exemple, la chaîne "panorama" peut être transformée en "paronomase" à l'aide des cinq opérations suivantes :

1. parorama (substitution de "n" en "r")

2. paronama (substitution de "r" en "n")

3. paronoma (substitution de "a" en "o")

4. paronomas (ajout d'un "s")

5. paronomase (ajout d'un "e")

On peut retrouver ce résultat avec l'algorithme de Levenshtein et vérifier qu'il s'agit bien d'une transformation de coût minimal. Il s'agit de remplir la matrice suivante :

Pour chaque case M[i, j], i et j>0, la valeur affectée est le minimum entre :

• M[i-1, j] + 1 (case directement à gauche) ;

• M[i, j-1] + 1 (case directement en haut) ;

• M[i-1,j-1] + 0 si les deux caractères sont égaux, M[i-1,j-1] + 1 sinon.

La dernière case de la matrice donne la distance d'édition entre C1 et C2, qui est bien celle de la transformation que nous avions proposée. En allant jusqu'à la dernière case tout en choisissant à chaque pas la case suivante la moins coûteuse, on trouve un ensemble minimal d'opérations :

• un saut de colonne (de gauche à droite), par exemple de M[8, 8] = 3 à M[8, 9] = 4, correspond à un ajout, ici l'ajout d'un "s" ;

• un saut de ligne (de haut en bas), inversement, correspond à une suppression ;

• un saut de ligne et de colonne (case juste en bas à droite), par exemple de M[2, 2] = 0 à M[3, 3] = 1, correspond à une substitution, ici la substitution de "n" en "r".

Le chemin mis en exergue dans la matrice correspond aux opérations proposées intuitivement plus haut. Cependant, d'autres chemins de même distance sont possibles.

Le problème de la plus longue sous-séquence commune (LCS pour Longest Common Subsequence) correspond à la recherche de l'edit script le plus court entre deux chaînes en termes d'ajout et de suppression (Myers, 1986^[2]). Contrairement à la distance de Levenshtein, les substitutions ne sont pas considérées ici. Par exemple, la LCS entre les chaînes "panorama" et "paronomase" est "panoma", d'après le résultat de l'algorithme de Myers (ibid.^[2]) implémenté dans la librairie google-diff-match-patch (Fraser) :

• panorama

• paronomase

D'où l'edit script minimal suivant pour transformer la première chaîne en la seconde :

• paronorama (insertion de "ro")

• parono|ma (suppression de "ra")

• paronomase (insertion de "se").

Les diffs permettant de comparer deux fichiers texte (diff textuel), c'est-à-dire deux séquences de caractères encodés en ASCII ou en Unicode par exemple, s'appuient généralement sur la recherche de la LCS entre ces deux séquences pour calculer le delta. Dans l'affichage ci-dessous, qui résulte de l'application de google-diff (s'appuyant sur l'algorithme de Myers (1986^[2])) à notre exemple, la LCS correspond aux caractères sur fond blanc tandis que les différences sont sur fond coloré. Notons que les fins de ligne sont également indiquées comme caractères, appartenant à la LCS ou non.

Ce résultat est assez proche de la troisième forme différentielle (diff orienté caractères) que nous avions proposée plus haut. Toutefois, concernant la troisième ligne, on remarque un affichage peu lisible à cause de lettres communes entre "alors" et "le message". En effet, l'intérêt d'un edit script minimal entre deux fichiers F1 et F2 est avant tout d'avoir de meilleures performances lors de la transformation de F1 en F2 par le patch, plus que de permettre la bonne lisibilité de la forme différentielle. Pour améliorer la sémantique des différences, Fraser (2009^[3]) propose un post-traitement de l'edit script permettant d'étendre les différences aux "petites parties communes" qu'elles encadrent (principe du semantic cleanup). Par exemple, l'application de ce post-traitement avec google-diff donne la ligne suivante pour notre exemple :

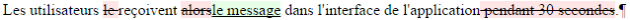
Le diff orienté lignes, tel que nous l'avons vu plus haut avec la commande Unix diff (Hunt&McIlroy, 1976^[4]), est un cas particulier de diff textuel dans lequel la LCS est recherchée au niveau des lignes et non au niveau des caractères. En ASCII par exemple, les lignes sont les séquences de caractères délimitées par la combinaison CR+LF (caractères spéciaux pour indiquer un retour chariot puis un saut de ligne, unifiés en un seul caractère CRLF sous Windows). Dans un diff orienté lignes, chaque ligne est préalablement codée sur un seul nombre par une fonction de hachage. Celle-ci assure que deux lignes identiques seront codées de la même façon, mais deux lignes non-identiques peuvent théoriquement être codées par le même nombre : en effet, la fonction de hachage n'est pas injective. Cependant, plus le nombre d'octets sur lequel est codée la valeur de hachage est grand, moins ces cas de "collision" sont probables. Par ailleurs, des mécanismes existent pour repérer de telles situations (ibid.^[4]). La LCS est alors recherchée sur les deux séquences de lignes codées, et les différences qui en résultent représentent des ajouts et suppressions de lignes. Sur notre exemple, la fonction de hachage pourrait transformer les deux versions ainsi :

1. 123

2. 1453

D'où la LCS "13" et l'edit script composé de la suppression de "2" et l'insertion de "4" et "5" à la place.

Un arbre est une structure de données composée de nœuds ayant les propriétés suivantes :

• chaque nœud est décrit par un label (une chaîne de caractère) ;

• chaque nœud peut contenir plusieurs nœuds enfants ;

• chaque nœud a au plus un parent ;

• un nœud sans enfant est une feuille, ou nœud terminal ;

• le nœud racine est l'ancêtre de tous les nœuds et est le seul à ne pas avoir de parent.

Outre la relation parent/enfant, les nœuds peuvent être frères (même parent), ancêtre/descendant, cousins, oncle/neveu, etc.. De plus, un arbre dans lequel les nœuds enfants se lisent dans un certain ordre (de gauche à droite) est dit ordonné.

Les opérations d'édition sur un arbre ne sont pas de même nature que les opérations résultant de la recherche de la LCS de deux chaînes. En effet, elles portent sur les nœuds de l'arbre et prennent en compte les relations hiérarchiques (parent/enfant) entre ces nœuds. La notion de distance entre deux arbres ordonnés a été introduite par Tai (1979^[5]), qui redéfinit les opérations d'insertion, de suppression et de substitution dans ce cadre :

• une insertion d'un nœud N1 au niveau d'un nœud N2 correspond au fait que le parent de N2 devienne celui de N1 et que N1 devienne le parent de N2 (et l'ancêtre de tous les nœuds du sous-arbre de N2) ;

• une suppression d'un nœud N correspond au rattachement de ses enfants au parent de N (en respectant l'ordre par rapport aux nœuds frères de N) ;

• une substitution correspond au changement du label d'un nœud.

La LCS peut toujours s'appliquer à une linéarisation de l'arbre, mais avec une expression des différences plus pauvre qu'avec les opérations d'édition ci-dessus.