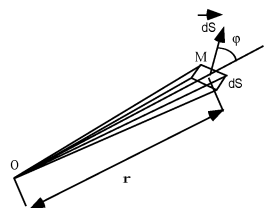
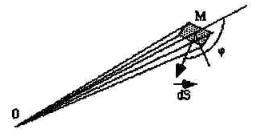
Angle solide sous lequel on voit une surface infiniment petite dS depuis un point O

Quel est l'angle solide sous lequel on voit une surface infiniment petite depuis un point d'observation ?

Angle solide sous lequel on voit une surface élémentaire dS depuis un point O

Soit 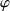l'angle que font la droite 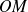et un vecteur 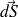perpendiculaire à la surface 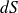en son milieu .

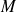Il s'agit bien sûr de l'angle solide du cône de sommet 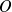s'appuyant sur les cotés de la surface .

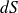Pour calculer cet angle solide 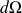, nous allons appliquer la définition précédente et calculer la surface délimitée par notre cône sur une sphère de centre 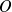et passant par .

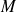Comme l'angle solide 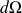est infiniment petit, cette surface élémentaire est assimilable à sa projection sur le plan tangeant à la sphère en ce point 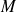. Elle vaut donc 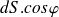et on en déduit :

Angle solide élémentaire négatif

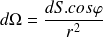
On voit que si l'angle 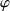est inférieur à 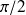alors 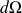est positif : le regard a traversé la surface dans le sens de l'orientation choisie. Si l'angle 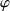est supérieur à 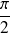, 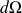est négatif : le regard a traversé la surface dans le sens opposé à celui de l'orientation choisie. On voit la surface à l'envers. L'angle solide algébrique associé à la surface orientée est ici négatif, parcequ'on regarde la surface à l'envers.