Surface d'un conducteur en équilibre

Puisque tout le conducteur est à un même potentiel, sa surface est une surface équipotentielle. Donc, le champ électrique à la surface est perpendiculaire à cette surface.

Nous avons dit précédemment que les charges sont immobiles parce qu'elles ne subissent pas de forces. Cela est vrai au milieu du conducteur. Il existe un endroit où les charges peuvent subir des forces sans pour autant se déplacer, c'est lorsque ces forces sont perpendiculaires à la surface et dirigées vers l'extérieur. Elles les plaquent sur la surface. Cela est donc conforme à l'existence d'un champ électrique à la surface du conducteur, orthogonal à la surface. Cela prouve également qu'à la surface du conducteur, il peut exister une densité de charges non nulle.

Les charges d'un conducteur en équilibre ne peuvent exister qu'à sa surface. On peut définir la densité surfacique de charges :

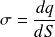
Puisque la seule force pouvant exister doit plaquer les charges sur la surface, il faut que le champ à la surface 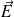soit dirigé vers l'extérieur si les charges surfaciques sont positives, et vers l'intérieur si elles sont négatives.

Les lignes de champ sont donc perpendiculaires à la surface du conducteur.

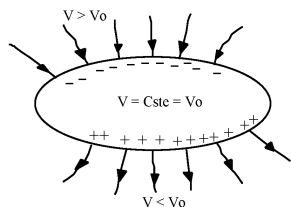
Là où les charges surfaciques sont positives, ces lignes de champ sortent.

Dans le cas contraire, elles entrent.

Une ligne de champ qui sort d'un conducteur en équilibre ne peut pas y revenir en un autre point, même si, en cet autre point, les charges surfaciques sont négatives. En effet, on sait que les lignes de champ se dirigent dans le sens des potentiels décroissants. Or tout le conducteur est équipotentiel.