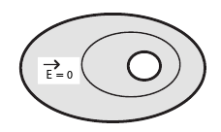
Cas d'un conducteur comportant une cavité vide

Imaginons un conducteur en équilibre électrostatique contenant une cavité vide. A priori, il pourrait exister des charges sur la surface de la cavité.

Puisque 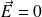dans le conducteur, l'application du théorème de Gauss à une surface fermée entourant la cavité et située dans C montre qu'il n'y en a pas, ou du moins que la somme des charges portées par la paroi de la cavité est nulle.

Or, s'il existait par endroit des répartitions surfaciques de charges positives ou négatives, il en sortirait des lignes de champ. Ces lignes de champ ne pourraient que revenir sur le même conducteur et nous avons vu que cela est impossible.

La surface de la cavité est une équipotentielle. Comme celle ci ne contient pas de charges, le potentiel ne peut pas y passer par un maximum, ni par un minimum. Il est donc constant et égal à celui du conducteur. Et puisque 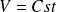dans la cavité, on en déduit que .

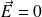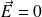à l'intérieur de la cavité.

Il n'y a pas de charges sur la surface interne de la cavité.

Toute la cavité est au même potentiel que le conducteur.