Chapitre 2 : Notions de métrologie

L'incertitude-type de type A est déterminée par une analyse statistique d'un ensemble de valeurs xi du mesurande obtenues dans les conditions de répétabilité (voir définition au début du chapitre). En effet, les valeurs des observations individuelles diffèrent à cause des erreurs aléatoires. Si on considère que l'on a réalisé une série de n mesurages, on a donc obtenue n valeurs de x_i ; on peut alors calculer la moyenne arithmétique de ces n valeurs de x_i que l'on notera \(\bar{x}\). Si on se place dans la situation idéale où le mesurage n'est affecté d'aucune erreur systématique, alors la valeur moyenne \(\bar{x}\) représente la meilleure estimation de la valeur vraie du mesurande ; on est alors dans la situation décrite par la cible de droite sur la figure précédente^[1] . Dans ce cas, c'est la dispersion des points autour de la moyenne qui va permettre de déterminer l'incertitude du mesurage.

La manière la plus simple pour calculer l'incertitude à partir de l'ensemble des valeurs du mesurande est d'utiliser la demi-étendue.

L'étendue de la mesure est égale à la différence entre la valeur la plus grande et la valeur la plus petite du mesurande. La demi-étendue est donc la moitié de la valeur de cette différence. Cette méthode conduit à une valeur d'incertitude relativement grande qui présente l'avantage de tenir compte de toutes les valeurs mesurées mais qui présente le désavantage de ne pas tenir compte de la distribution des valeurs à l'intérieur de la plage de mesure. En particulier, les points aberrants affectent énormément la valeur de l'étendue. Cette méthode est donc à proscrire.

On préférera utiliser une autre grandeur statistique qui s'appelle l'écart-type dont l'avantage est de tenir compte de la distribution des valeurs à l'intérieur de la plage de mesure; en effet, les points extrêmes affectent moins l'écart-type que la demi-étendue de mesure. L'écart-type s d'une série de n mesurages est donné par la formule suivante:

\(s=\sqrt{\frac{\sum\limits_{i=1}^{n}{{{({{x}_{i}}-\bar{x})}^{2}}}}{n-1}}\)

où les x_i sont les résultats des différents mesurages et \(\bar{x}\) est la moyenne arithmétique des n résultats considérés.

En général, la distribution des valeurs obtenues xi autour de la valeur moyenne suit une loi normale (à condition que le nombre de mesurages n soit très grand). La loi normale est une loi statistique qui décrit la répartition des valeurs autour de la moyenne et dont la représentation mathématique est la suivante :

\(n({{x}_{i}})=\frac{n}{s\sqrt{2\pi }}\exp \left[ -\frac{{{({{x}_{i}}-\bar{x})}^{2}}}{2{{s}^{2}}} \right]\)

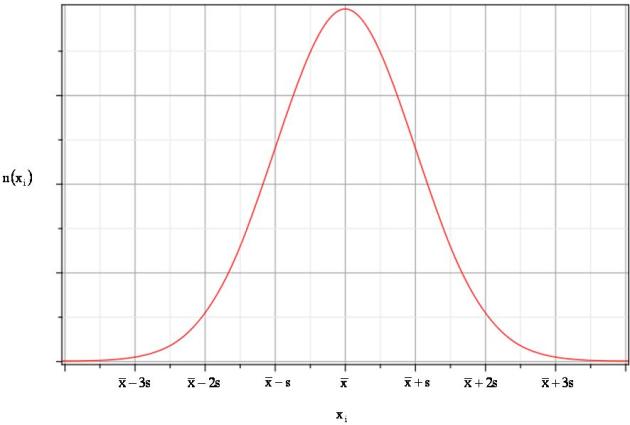
La valeur n(xi) représente le nombre de valeurs xi obtenues sur les n mesurages effectués. Cette loi mathématique conduit à la répartition des valeurs données sur la figure :

Sur ce graphique, on remarque que c'est la valeur moyenne \(\bar{x}\) qui présente la plus grande occurrence et qu'au fur et à mesure que l'on s'écarte de cette valeur moyenne, le nombre d'occurrence diminue. L'écart-type s représente "la largeur" de la courbe de la figure 3. Plus la valeur de s est grande, plus la courbe s'élargit. Ceci démontre bien l'intérêt d'utiliser l'écart type plutôt que la demi-étendue pour déterminer une incertitude de type A, car on va alors tenir compte de la distribution des valeurs à l'intérieur de la plage de mesure.

Maintenant, si on admet que la distribution statistique de la figure est respectée, alors, lorsqu'on effectue un mesurage unique, la valeur trouvée suit la distribution statistique donnée par cette courbe.

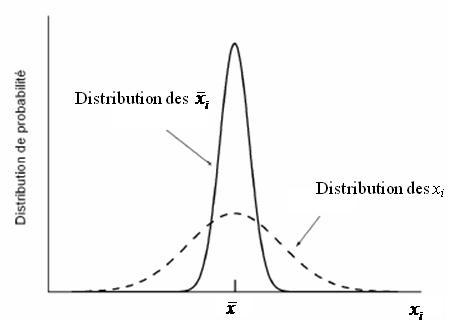
En effectuant n mesurages, les valeurs obtenues se répartissent aléatoirement sur cette courbe. Donc, lorsqu'on prend la valeur moyenne de ces n mesures, les écarts à la valeur vraie se compensent statistiquement, avec d'autant plus d'efficacité que n est grand. Ainsi, cette valeur moyenne que l'on note \({{\bar{x}}_{1}}\) est proche de la valeur \(\bar{x}\) sur la figure. Si on réalise une nouvelle série de n mesurages et qu'on en réalise la moyenne arithmétique, on obtiendra une deuxième valeur de la moyenne \({{\bar{x}}_{2}}\) également proche de \(\bar{x}\). On peut réitérer ceci un grand nombre de fois puis tracer la répartition des valeurs \({{\bar{x}}_{i}}\). Ceci est schématisé sur la figure suivante^[2] : La courbe en pointillé représente la distribution des valeurs x_i et la courbe en trait plein représente la distribution des valeurs \({{\bar{x}}_{i}}\). Cette figure illustre bien le fait qu'en réalisant des moyennes arithmétiques sur n mesurages, on a une compensation des erreurs. Au final, on constate que la dispersion des valeurs moyennes est plus faible que la dispersion des valeurs individuelles. C'est donc la "la largeur" de la courbe de répartition des valeurs moyennes qui va être utilisée pour quantifier l'incertitude-type de type A. Cette largeur est appelée écart-type à la moyenne et se calcule à partir de l'écart-type s :

\({{s}_{{\bar{x}}}}=\frac{s}{\sqrt{n}}=\sqrt{\frac{\sum\limits_{i=1}^{n}{{{({{x}_{i}}-\bar{x})}^{2}}}}{n\ (n-1)}}\)

La valeur de \({{s}_{{\bar{x}}}}\) est appelée incertitude-type de type A.

L'autre point important à noter est que lorsque l'on définit l'incertitude-type de type A par l'écart type à la moyenne \({{s}_{{\bar{x}}}}\), cela signifie que l'on considère que la valeur de x se situe entre deux valeurs extrêmes qui sont \(bar{x}-{{s}_{{\bar{x}}}}\) et \(\bar{x}+{{s}_{{\bar{x}}}}\), alors on exclut de nombreuses valeurs qui se situent en dehors de cette plage ; on aura alors un intervalle de confiance assez faible. En fait, sir le nombre de mesurages n est infini, on a 68% de chance que la valeur de x se situe dans l'intervalle \([\bar{x}-{{s}_{{\bar{x}}}}\ ;\ \bar{x}+{{s}_{{\bar{x}}}}]\). Généralement, on ne se contente pas de cet intervalle de confiance et on va l'augmenter. Voici ce que l'on obtient pour les intervalles couramment utilisés en considérant que n est tends vers l'infini :

Pour\( \Delta x=\pm {{s}_{{\bar{x}}}}\) (soit l'intervalle \([\bar{x}-{{s}_{{\bar{x}}}}\ ;\ \bar{x}+{{s}_{{\bar{x}}}}]\)), le niveau de confiance est de 68%

Pour\( \Delta x=\pm 2{{s}_{{\bar{x}}}}\) (soit l'intervalle\( [\bar{x}-2{{s}_{{\bar{x}}}}\ ;\ \bar{x}+2{{s}_{{\bar{x}}}}]\)), le niveau de confiance est de 95%

Pour \(\Delta x=\pm 3{{s}_{{\bar{x}}}}\) (soit l'intervalle \([\bar{x}-3{{s}_{{\bar{x}}}}\ ;\ \bar{x}+3{{s}_{{\bar{x}}}}]\)), le niveau de confiance est de 99,73%

En général, on se contente d'un niveau de confiance de 95%. Pour autant, dans un contexte industriel, on peut chercher à relever ce niveau de confiance. Par exemple, imaginons qu'une entreprise produise des pièces dont la longueur ℓ doit avoir une précision Δℓ fixée par les exigences de ses clients ; l'outil de production, après réglage, produit des pièces avec une dispersion sl (écart-type à la moyenne) autour de la valeur moyenne ℓ ; si Δℓ = 2·sl, cela signifie que pour un milliard de pièces produites, 50 millions (soit 5%) iront au rebut, ce qui est énorme ; si Δℓ = 3·sl (grâce à une optimisation de l'outil de production, l'entreprise a divisé sl par un facteur 1,5), alors pour un milliard de pièces produites, 2,7 millions iront au rebut (soit 0,27%), ce qui est encore important ; si elle réussit à diminuer sl encore de moitié, on aura alors Δℓ = 6·sl, soit un taux de rebut de 2·10-9 (0,000 000 2 %), et alors deux pièces iront au rebut par milliard produit, ce qui devient excellent.

Le problème est que pour pouvoir utiliser ces intervalles de confiance, il faut que la loi normale soit respectée par la collection de valeurs obtenues par mesurage, ce qui implique que le nombre de mesurage doit être suffisamment important.

Lorsque le nombre de valeurs obtenues est trop faible pour que la courbe de distribution des valeurs respecte la loi Gaussienne, il reste possible d'utiliser la valeur de l'écart-type à la moyenne, mais il faut apporter un terme correctif qui va permettre d'élargir l'intervalle. On peut pour cela utiliser le coefficient k de Student. On obtient alors l'incertitude en multipliant l'écart type à la moyenne \({{s}_{{\bar{x}}}}\) par le coefficient de Student k :

\(\Delta x=\pm ({{s}_{{\bar{x}}}}\times k)\)

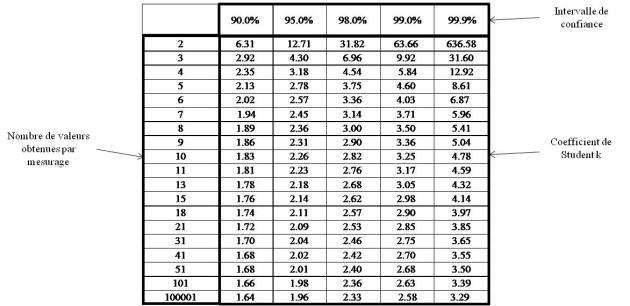
La valeur du coefficient k dépends de l'intervalle de confiance que l'on souhaite, et du nombre de valeurs sur lequel l'écart type à la moyenne a été calculé. Le tableau suivant fournit les valeur de k :

Lorsque l'on utilise le facteur d'élargissement k, on obtient ce que l'on nomme une incertitude élargie de type A.