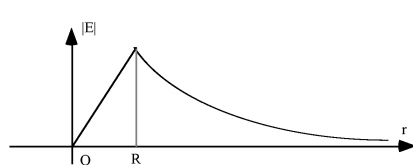
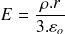Application du Théorème de Gauss : un exemple
Ce théorème permet un calcul aisé du champ électrique dans tous les cas où il existe une symétrie.
Par exemple, si nous reprenons le cas d'une charge sphérique de rayon
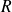t de densité volumique
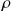, par raison de symétrie il est évident que le champ
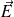ne peut être que radial, et que son amplitude ne peut dépendre que de la distance
par rapport au centre de la sphère.
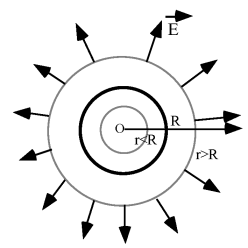
Si on choisit une surface de Gauss
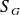qui soit une sphère à la charge et de rayon
, le flux de
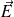vaut
.
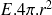D'après le théorème de Gauss, ce flux est aussi égal à la somme des charges internes à
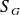divisée par
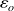plus la somme des charges surfaciques divisée par
.
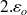Il n'y a pas de charges à la surface de
.
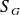Si
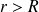, toute la charge
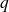est interne à
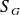. Donc
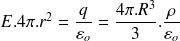
D'où
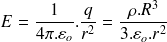
Si
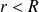, les charges internes à
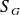valent
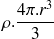
Donc
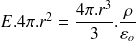
D'où
