Champ créé par un plan uniformément chargé
Question
Calculer le champ créé en tout point de l'espace par un plan uniformément chargé : densité de charges
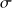 .
.
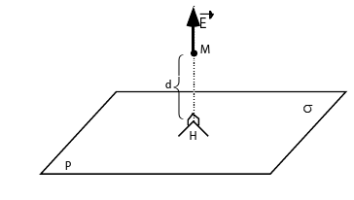
Par raison de symétrie, le champ
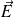 ne peut être que perpendiculaire au plan et son module ne peut dépendre que de la distance du point
ne peut être que perpendiculaire au plan et son module ne peut dépendre que de la distance du point
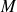 au plan
au plan
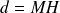 .
.
Toujours par symétrie, à la distance
 ,
,
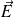 est égal et opposé.
est égal et opposé.
Etant donné la symétrie du problème, il semble que la meilleure méthode pour calculer
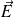 soit l'application du théorème de Gauss.
soit l'application du théorème de Gauss.
Une surface de Gauss idéale est une surface sur laquelle
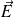 est constant et perpendiculaire ou au contraire
est constant et perpendiculaire ou au contraire
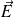 parallèle.
parallèle.
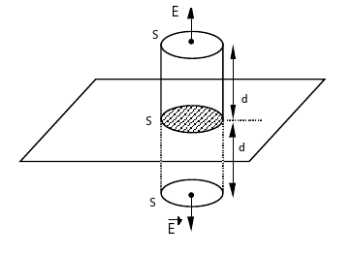
Ici, on peut choisir comme surface de Gauss un cylindre qui aurait des parois perpendiculaires au plan (donc parallèles à
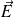 ) et des extrémités parallèles au plan et situées de part et d'autre à la même distance
) et des extrémités parallèles au plan et situées de part et d'autre à la même distance
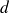 . Ainsi, sur ces extrémités, le champ sera perpendiculaire à la surface, sortant et d'amplitude constante.
. Ainsi, sur ces extrémités, le champ sera perpendiculaire à la surface, sortant et d'amplitude constante.
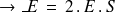 .
.
La charge contenue à l'intérieur de cette surface de Gauss vaut
 .
.
Donc
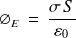
Donc

Le champ est uniforme et indépendant de la distance
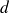 .
.
