Condensateur sphérique
Le conducteur
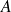est une sphère, la paroi intérieure de
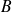est une sphère concentrique, la surface extérieure peut être quelconque.
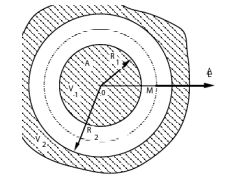
Par raison de symétrie, le champ en un point
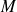pris entre les armatures est dirigé suivant l'axe de
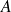vers
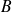, son module est le même en tous points de la sphère
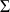, à savoir
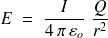
mais, puisque le champ est radial,
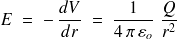
et en intégrant entre les limite
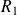et
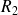, rayons de
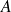et de
,
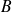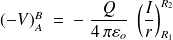
soit
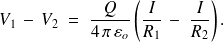
La capacité
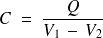
du condensateur sphérique est donc
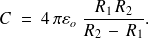
Remarque : Si la distance
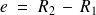entre les armatures est petite devant
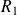et
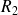, on a, en posant
,
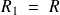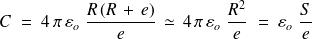
On suppose
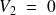et on calcule
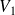en fonction de
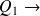On calcule la charge totale de l'armature interne
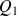et celle de l'armature externe
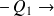influence totale.
Effet d'écran à l'extérieur, on ne sait pas ce qui se passe à l'intérieur.
Si
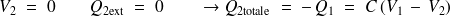
Si
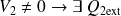se calcule comme dans l'exercice n°1
:
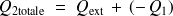
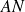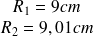
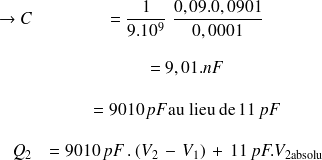
En général,
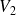est faible ou nul et ce qui nous intéresse, c'est
.
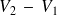Le but du condensateur, c'est de faire du stockage de charges.
