Champ électrique créé sur son axe par un disque uniformément chargé
Question
Calculer par une intégrale simple le champ électrique créé sur son axe par un disque de rayon
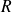 , portant une charge surfacique
, portant une charge surfacique
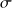 .
.
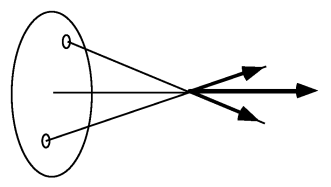
Etant donnée la symétrie du problème,
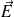 est axial, car à tout morceau élémentaire de surface
est axial, car à tout morceau élémentaire de surface
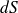 , on peut associer un morceau identique symétrique par rapport à l'axe. La résultante des deux champs générés est portée par l'axe.
, on peut associer un morceau identique symétrique par rapport à l'axe. La résultante des deux champs générés est portée par l'axe.
Soit
 la distance entre le point
la distance entre le point
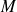 de l'axe et le centre du cercle.
de l'axe et le centre du cercle.
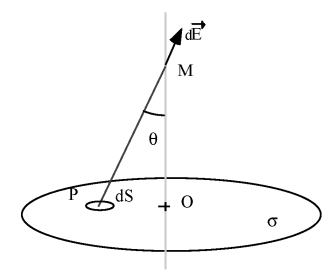
Un élément de surface
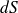 crée un champ
crée un champ
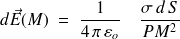
Le champ résultant étant porté par l'axe, il faut faire la somme des composantes axiales des champs élémentaires.
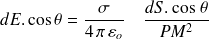
Or
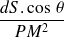
est l'angle solide
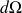 sous lequel on voit la petite surface
sous lequel on voit la petite surface
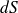 depuis le point
depuis le point
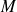 .
.
Donc
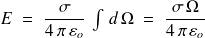
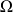 étant l'angle solide sous lequel est vu le disque depuis le point
étant l'angle solide sous lequel est vu le disque depuis le point
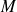 .
.
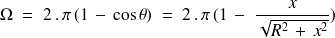
D'où
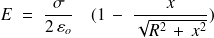
On peut mener le calcul sans remarquer que l'on a l'expression d'un angle solide :
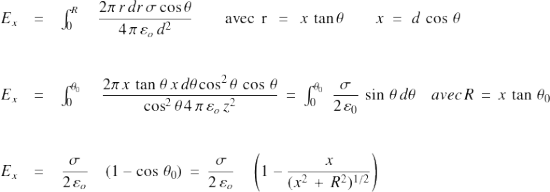
Trouver la forme asymptotique lorsque
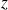 , la distance du point au centre de la sphère,est beaucoup plus petite ou beaucoup plus grande que
, la distance du point au centre de la sphère,est beaucoup plus petite ou beaucoup plus grande que
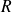 .
.
Très loin du disque,
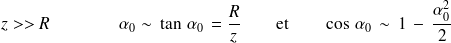
D'où
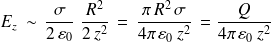
où
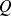 est la charge totale du disque.
est la charge totale du disque.
Le champ à grande distance est donc le même que celui d'une charge ponctuelle
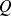 , ce qui est évident.
, ce qui est évident.
Très près du disque,
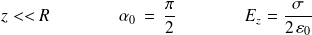
Le champ ne dépend que de
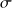 .
.
En déduire le champ créé par un plan infini chargé uniformément.
Un plan infini, uniformément chargé peut être assimilé à un disque de rayon très grand, alors le champ est uniforme de valeur
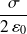 , symétrique par rapport au plan. Le champ est alors uniforme dans tout l'espace !!
, symétrique par rapport au plan. Le champ est alors uniforme dans tout l'espace !!
