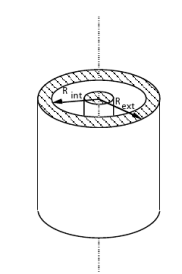
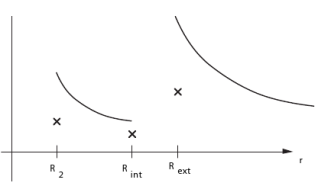
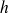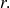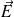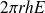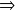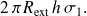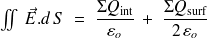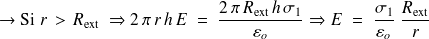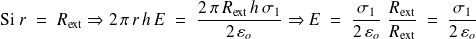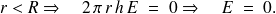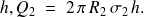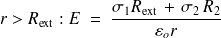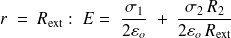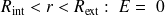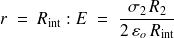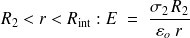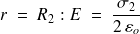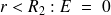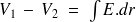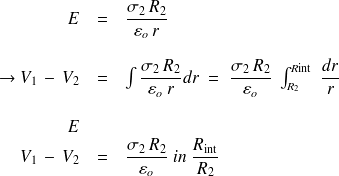Etant donné la symétrie axiale du problème, le champ
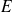 ne peut être radial et son amplitude ne dépend que de la distance à l'axe. C'est donc un cas idéal pour l'application du théorème de Gauss en choisissant comme surface de Gauss un cylindre coaxial au tube de hauteur quelconque
ne peut être radial et son amplitude ne dépend que de la distance à l'axe. C'est donc un cas idéal pour l'application du théorème de Gauss en choisissant comme surface de Gauss un cylindre coaxial au tube de hauteur quelconque
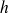 et de rayon
et de rayon
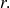
Le flux de
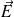 à travers cette surface vaudra
à travers cette surface vaudra
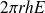 car, sous les parois,
car, sous les parois,
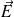 est perpendiculaire à la surface et d'amplitude constante et sur les extrémités,
est perpendiculaire à la surface et d'amplitude constante et sur les extrémités,
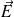 est parallèle à la surface de Gauss.
est parallèle à la surface de Gauss.
1) Quand il n'y a que le tube seul, on sait qu'il ne peut porter de charges qu'à sa surface extérieure
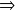 Sur une hauteur
Sur une hauteur
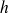 , il porte la charge
, il porte la charge
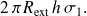
 Appliquons le théorème de Gauss
Appliquons le théorème de Gauss
(Ce résultat est connu pour la surface de tout conducteur en équilibre).
Si
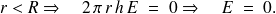 Encore un résultat connu.
Encore un résultat connu.
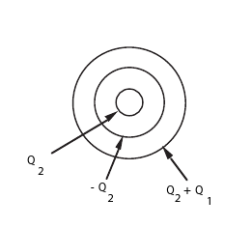
2) Si on introduit une barre chargée à l'intérieur, il y a influence totale et il apparaît une charge identique sur la paroi interne du tube
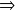 La surface externe voit donc sa charge totale cro”tre de la même quantité.
La surface externe voit donc sa charge totale cro”tre de la même quantité.
 Sur une hauteur
Sur une hauteur
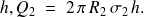
Donc, à l'extérieur du tube
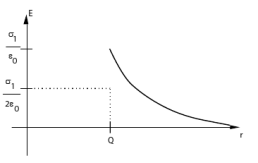
3) En appliquant le théorème de Gauss, on trouve :
-
Pour
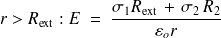
-
Pour
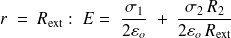
-
Pour
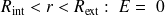
-
Pour
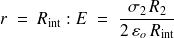
-
Pour
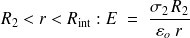
-
Pour
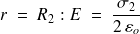
-
Pour
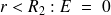
4) Entre la barre et le tube
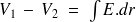
Or
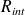 et de rayon extérieur
et de rayon extérieur
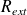 . Ce tube porte une densité surfacique de charges
. Ce tube porte une densité surfacique de charges
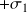 .
.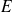 en tout point de l'espace.
en tout point de l'espace. 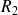 , concentrique du tube, portant une densité surfacique de charge
, concentrique du tube, portant une densité surfacique de charge
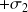 .
.