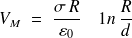Problème à symétrie axiale
Question
Calculez le champ et le potentiel créés en tout point de l'espace par un tube portant une charge uniformément répartie à sa surface extérieure
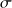 . Sa longueur est supposée infinie.
. Sa longueur est supposée infinie.
Le problème présente une symétrie évidente
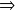 le champ électrique
le champ électrique
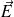 en tout point ne peut qu'être perpendiculaire à l'axe du tube et son module ne peut dépendre que de la distance à l'axe :
en tout point ne peut qu'être perpendiculaire à l'axe du tube et son module ne peut dépendre que de la distance à l'axe :
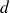 .
.
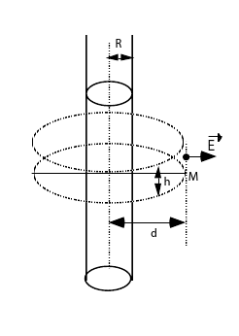
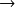 La meilleure méthode pour calculer
La meilleure méthode pour calculer
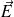 est l'application du théorème de Gauss.
est l'application du théorème de Gauss.
Comme surface de Gauss, on choisit un cylindre coaxial au tube et dont les extrémités sont perpendiculaires à l'axe.
Ainsi, sur les extrémités du cylindre,
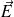 est parallèle à la surface et le flux correspondant est nul.
est parallèle à la surface et le flux correspondant est nul.
Par contre, sur les parois du cylindre,
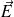 est perpendiculaire à la surface de Gauss et son module est constant.
est perpendiculaire à la surface de Gauss et son module est constant.
Donc
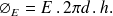
¥ Si M est à l'intérieur du tube, la surface de Gauss ne contient aucune charge.
Donc
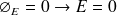
¥ Si M est sur la surface du tube
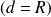 alors les charges du tube sont situées sur la surface de Gauss.
alors les charges du tube sont situées sur la surface de Gauss.
Dans ce cas, l'application du théorème de Gauss nous donne :
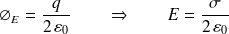
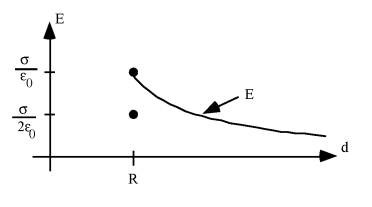
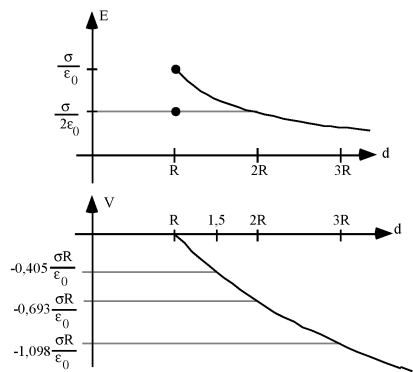
Le potentiel est calculé par application de sa définition
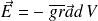
Si on cherche le potentiel absolu (
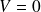 à l'infini) on calculera
à l'infini) on calculera
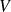 en
en
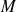 par :
par :
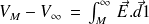
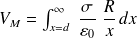
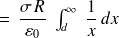
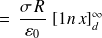
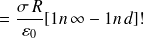
On voit qu'on arrive à une difficulté : c'est normal car on a par hypothèse des charges à l'infini.
On ne peut donc pas supposer que le potentiel y est nul.
Il serait préférable par exemple de fixer un potentiel arbitraire à une distance
 et de calculer ensuite le potentiel en un point
et de calculer ensuite le potentiel en un point
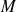 par différence :
par différence :
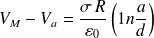
Si on veut, on peut aussi prendre comme origine des potentiels l'axe du tube.
On aura alors, à l'intérieur,
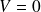 et à l'extérieur,
et à l'extérieur,