Conception de formes de relecture dans les chaînes éditoriales numériques

Soit un fragment et C un contenu quelconque de ce fragment. On note αF1(C) (resp. αF2(C)) l'ensemble constitué des contenus enfants de C fléchés pour D1 (resp. D2), et βF1(C) (resp. βF2(C)) l'ensemble constitué des contenus descendants de C fléchés pour D1 (resp. D2). Si C est fléché pour D1 et D2, on dira que :

1. C est divergeant si αF1(C) ⋂ αF2(C) = ∅ (aucun contenu enfant n'est fléché pour D1 et D2 à la fois) ;

2. C n'a pas de déclinaison sous-jacente si βF1(C) = βF2(C).

On note πF1(C), πF2(C) et πF1,F2(C) les projections de C respectivement sur F1, F2, F1 et F2.

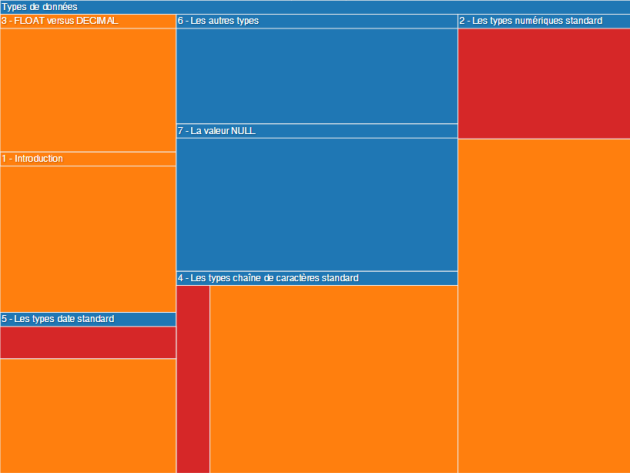
Le treemap suivant représente le grain "Types de données" vu précédemment^[1] :

On établit les ensembles suivants :

• αs0 (resp. αc0), soit l'ensemble des enfants du grain fléchés pour la version standard (resp. version courte) :

  • αs0 = {1, 2, 3, 4, 5, 6, 7}

  • αc0 = {2, 4, 5, 6, 7}

• βs0 (resp. βc0), soit l'ensemble des descendants du grain fléchés pour la version standard (resp. version courte) :

  • βs0 = {1, 1.1, 2, 2.2, 3, 3.1, 4, 4.2, 5, 5.2, 6, 6.1, 7, 7.1}

  • βc0 = {2, 2.1, 4, 4.1, 5, 5.1, 6, 6.1, 7, 7.1}

• αsi, αci, βsi, βci (i > 0), c'est-à-dire l'équivalent des ensembles précédant au niveau des balises pédagogiques, prises dans l'ordre des i :

  • αs1 = {1.1}

  • αs3 = {3.1}

  • αc1 = αc3 = ∅

  • αs2 = {2.2}

  • αc2 = {2.1}

  • αs4 = {4.2}

  • αc4 = {4.1}

  • αs5 = {5.2}

  • αc5 = {5.1}

  • αs6 = {6.1}

  • αc6 = {6.1}

  • αs7 = {7.1}

  • αc7 = {7.1}

  • pour tous les βsi (resp. βci), i > 1 αsi = βsi (resp. αci = βci)

Nous déduisons de ces ensembles les propriétés suivantes :

• Le grain "Types de données" :

  • a des déclinaisons sous-jacentes ;

  • n'est pas divergeant (présence de balises pédagogiques communes) ;

• Les balises pédagogiques n°2, 4 et 5 :

  • ont des déclinaisons sous-jacentes ;

  • sont divergentes (il n'y a aucun contenu commun) ;

• Les balises pédagogiques n°6 et 7 :

  • n'ont pas de déclinaison sous-jacente ;

  • par conséquent, ne sont pas divergentes (elles sont chacune strictement identiques dans les deux versions).

Notons que l'on peut aussi repérer visuellement ces propriétés de la manière suivante :

• les contenus sans déclinaison sous-jacente sont les rectangles de label bleu imbriquant uniquement des rectangles bleus ;

• les contenus divergents sont les rectangles de label bleu n'imbriquant que des rectangles oranges ou rouges.

Soit un contenu C0 commun à D1 et D2 dont on supposera qu'il a des déclinaisons sous-jacentes et qu'il n'est pas divergeant. Pour chaque contenu enfant de C0, noté C, nous proposons de construire la tabulation de la manière suivante :

• si C est commun à D1 et D2 et sans déclinaison sous-jacente (exemples : BP n°6 et 7) : une ligne d'équivalence comportant πF1,F2(C) dans chaque case (à partir de C, D1 et D2 sont identiques "jusqu'au bout") ;

• si C est commun à D1 et D2 et divergeant (exemples : BP n°2, 4 et 5) : une ligne d'alternative opposant πF1(C) dans la case de gauche à πF2(C) dans la case de droite ;

• si C est fléché uniquement pour D1 (resp. D2) : une ligne opposant πF1(C) dans la case de gauche (resp. πF2(C) dans la case de droite) à une case vide dans la case de droite (resp. de gauche).