Conception de formes de relecture dans les chaînes éditoriales numériques

Soit un contenu C commun à D1 et D2, non-divergeant. On dira que C est partiellement divergeant si αF1(C) ≠ ∅ et αF2(C) ≠ ∅.

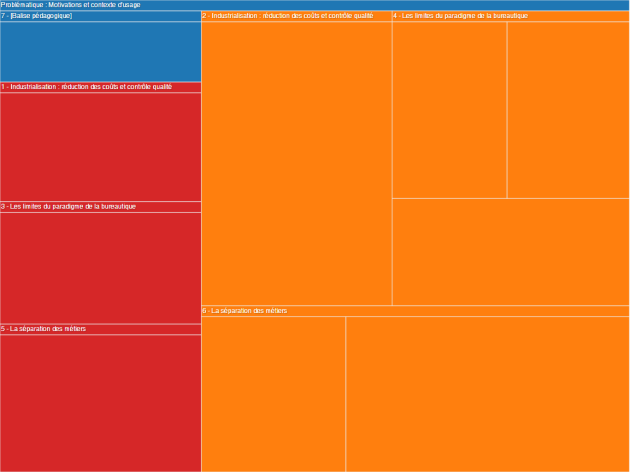
Le grain suivant est un exemple de contenu partiellement divergeant :

Il est possible de repérer visuellement ce type de contenu : il s'agit de rectangles de label bleu imbriquant un mélange de rectangles bleus, oranges et rouges.

Si l'on applique à ce grain l'algorithme de tabulation proposé plus haut, on obtient le résultat ci-dessous. Notons que cela produit un effet de "quinconce" sur les BP, ce qui rend la relecture plus difficile. Étant donné que le contenu diverge hormis au niveau de la dernière BP, il serait plus judicieux d'opposer les BP n°1, 3 et 5 d'une part aux BP n°2, 4 et 6 d'autre part, ceci afin de "condenser" la tabulation.

L'algorithme doit donc être complété en prenant en compte le cas des contenus partiellement divergeant. Une première solution consiste à projeter entièrement C (une ligne d'alternative opposant πF1(C) dans la case de gauche à πF2(C) dans la case de droite) :

Cette solution paraît bancale dans la mesure où elle mène potentiellement à des déphasages entre les contenus communs à D1 et D2 dans C.

Soit αF1(C, i, j) (resp. αF2(C, i, j)) l'ensemble constitué des contenus enfants de C fléchés pour D1 (resp. D2) entre les indices i et j. On définira également les projections locales de C, πF1(C, i, j) (resp. πF2(C, i, j)). Enfin, on appellera segment divergeant un couple (i, j) tel que :

• αF1(C, i, j) ⋂ αF2(C, i, j) = ∅

• le contenu à l'index i-1 (resp. j+1), s'il existe, est commun à D1 et D2.

Une seconde solution consiste à poser, pour tout segment divergeant (i, j) de C, une ligne d'alternative opposant πF1(C, i, j) dans la case de gauche à πF2(C, i, j) dans la case de droite :