Conception de formes de relecture dans les chaînes éditoriales numériques

Une première solution de linéarisation des parcours réticulaires d'un graphe consiste à générer un à un les différents parcours possibles de ce graphe. Cette solution est en revanche fortement limitée dans le cadre de la relecture, ces parcours étant en nombre élevé voire infini si le graphe comporte un circuit.

Une seconde solution s'inspire directement du lecteur, qui construit un parcours par choix successifs et élimination progressive des autres parcours possibles. Le parcours construit peut alors servir de référence pour les parcours qu'il reste à explorer. En référence aux notions de récit primaire (lu, vécu par le lecteur) et de récit secondaire (possible narratif prévu par l'auteur, mais éliminé par le lecteur), proposées par Clément dans ses travaux sur les structures arborescentes, nous parlerons d'une part de parcours primaire pour désigner le parcours construit par le relecteur, et d'autre part de parcours secondaires exprimés relativement au parcours primaire. Notons que l'adjectif "secondaire" n'est pas à comprendre ici comme un second niveau de discours inscrit dans le paratexte, mais bien comme un récit/parcours indépendant, qui aurait tout à fait pu être lu à la place du récit/parcours primaire.

Voici un exemple de parcours primaire possible, représenté en vert, dans le graphe d'Un conte à votre façon, ainsi que les parcours secondaires relatifs, représentés en gris :

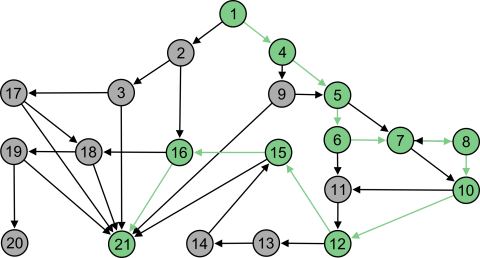
Un parcours primaire est signifiant pour une relecture linéaire en ce qu'il est un parcours possible du graphe (du moins, si ce parcours n'est pas signifiant, il permet de refléter un éventuel défaut de conception du document...).

Les liens éliminés dans la construction du parcours primaire sont à distinguer selon plusieurs types. Lorsque le nœud au bout du lien éliminé appartient au parcours, on dira que le lien est un saut si le nœud est rencontré plus loin dans le parcours, ou un retour s'il a déjà été rencontré (cas du circuit). Par exemple, le sous-parcours ci-dessous présente un saut de 7 à 10 et un retour de 8 à 7 :

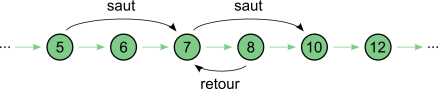
Si au contraire, le nœud au bout du lien éliminé n'appartient pas au parcours primaire, on parlera de divergence. Une divergence est de surcroît définitive si aucun nœud du parcours primaire n'est présent dans le sous-graphe lié. Autrement dit, un parcours secondaire est définitivement divergeant s'il ne converge pas in fine vers un nœud du parcours primaire. Par exemple, le parcours secondaire 1-2-3-17-18-19-21 est divergeant, tandis que 1-2-3-17-18-19-20 est définitivement divergeant :

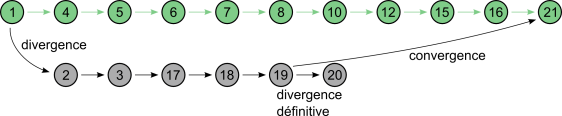
Notons que tous ces types de lien peuvent aussi exister au niveau d'un parcours secondaire.