Influence totale
On dit que deux conducteurs sont en influence totale si l'un (
) est à l'intérieur de l'autre (
).
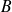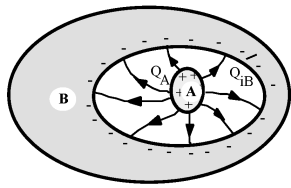
Toute ligne de champ qui sort de
ne peut aller que sur
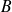. Toute la surface de
est élément correspondant de la surface interne de
.
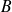porte donc une charge totale
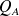égale et opposée à celle que porte la surface interne de
.
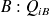Si on applique le théorème de Gauss pour calculer le champ
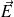à l'extérieur de
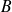, on voit que seules les charges
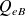situées sur la surface externe de
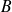interviennent puisque celles de la surface interne
sont compensées par celles
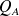que porte
. Donc, le champ électrique à l'extérieur de
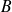ne dépend que de
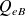; il en est bien sûr de même du potentiel.
Supposons que nous introduisions
chargé à l'intérieur de
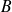. La paroi interne de
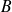se charge d'une quantité
.
-
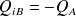Si
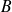reste isolée pendant l'expérience, sa charge totale ne peut pas changer. Donc la paroi externe de B voit sa charge surfacique augmenter de
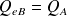qui s'ajoute donc à une éventuelle charge initiale
.
-
Si
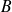a été maintenu à un potentiel constant, par exemple par une liaison à la masse, alors sa charge externe n'a pas changé. C'est donc qu'une quantité de charges
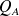s'est écoulée vers la masse par le dispositif de liaison.
La distribution de charges à l'intérieur de
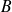dépend de la position de
dans la cavité.
Celles de la surface externe n'en dépend pas.
