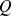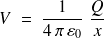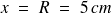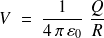Électricité
CoursOutils transverses
- Rappel de quelques notions mathématiques
- Électrostatique
- Phénomènes "électriques" - Electrisation par frottements
- Interactions électrostatiques - Approche quantitative - Champ électrique
- Potentiel électrostatique
- Flux de E à travers une surface fermée - Théorème de Gauss
- Conducteur seul en équilibre
- Ensemble de conducteurs en équilibre
- Influence entre deux conducteurs en équilibre
- Plan de masse ou terre
- Influence électrostatique sur un conducteur isolé
- Influence électrostatique sur un conducteur maintenu
- Conducteurs en équilibre
- Influence totale
- Superposition des états d'équilibre
- Capacité d'un conducteur seul
- Capacité d'une sphère
- Coefficients d'influence
- Condensateur
- Condensateur sphérique
- Condensateur cylindrique
- Echange de charges entre condensateurs
- Condensateurs en série et en paralèle.
- Electromètre à plateau
- Capacité d'un câble coaxial
- Condensateur tube
- Rigidité diélectrique
- Condensateur plan
- Condensateur papier
- Forces et énergie dans un condensateur.
- Influence de lames diélectriques ou conductrices dans un condensateur.
- Tenue en tension d'un condensateur
- Condensateur chimique
- Énergie stockée dans un condensateur chargé
- EXERCICES A RENDRE PAR ECRIT : SERIE 4
- Annexes