Condensateur cylindrique
L'armature interne et la paroi intérieure de l'armature externe sont des cylindres de révolution coaxiaux, la surface extérieure peut être quelconque.
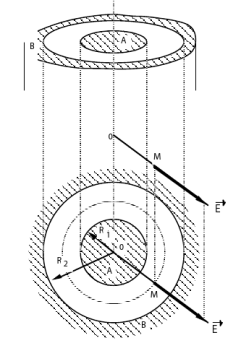
Si les cylindres sont indéfinis, le champ
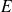en un point
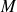est, par raison de symétrie, dirigé suivant l'axe
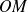. Considérons la portion de hauteur
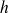comprise entre deux plans
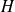et
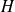' perpendiculaires à l'axe et soit
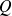la charge de
.
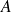Appliquons le théorème de Gauss à la surface formée par le cylindre de révolution de rayon
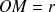, limité par
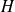et
:
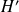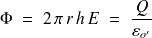
d'où
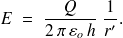
De
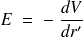on déduit
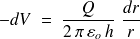, et en intégrant entre les limites
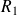et
:
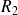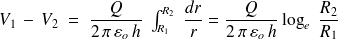
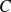étant la capacité du tronçon considéré, définie par
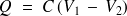, on a :
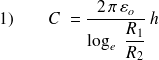
la capacité par unité de longueur comptée sur l'axe a pour expression
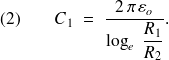
En réalité, les cylindres
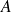et
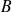ne sont pas indéfinis et des perturbations de champ se produisent au voisinage de leurs extrémités ; elles ont pour conséquence de modifier les expressions de
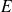, donc de
.
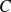Néanmoins, si la longueur des armatures est grande devant
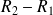, on peut, sans erreur appréciable, utiliser l'expression (1).
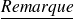: Si
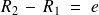est petit devant
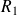, on peut écrire
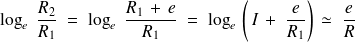
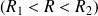et par conséquent
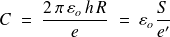
où
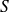est la surface latérale du cylindre
.
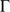