Énergie stockée dans un condensateur chargé

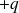Nous avons vu qu'un condensateur soumis à une différence de potentiel portait des charges et 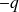sur ses armatures, avec la relation .

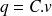Pour accroître de 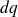la charge des armatures, il faut qu'une quantité 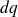de charges se déplacent et voient leur potentiel passer de zéro à v. On sait que pour un tel déplacement, il faut leur apporter une quantité d'énergie égale à

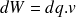
Or, si on apporte une quantité de charges supplémentaires 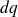, la différence de potentiel 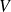s'accroît de 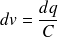Donc, on peut écrire 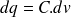et

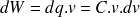
Par intégration, on peut en déduire la quantité totale d'énergie qu'il a fallu apporter pour amener la différence de potentiel aux bornes du condensateur de zéro à

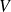
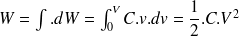
Si l'on relie ensuite entre elles les deux armatures par un fil conducteur, le condensateur va se décharger : les charges accumulées vont repartir. En faisant le même calcul que précédemment, on peut déterminer l'énergie que recevront les charges durant leur retour, pendant que la différence de potentiel entre les armatures va repasser de 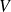à .

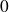On obtient :

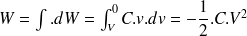
Ceci prouve que l'énergie fournie durant la charge était restée disponible et qu'elle est restituée lors de la décharge du condensateur.

Un condensateur est donc un réservoir d'énergie électrique.